
NATRAJ VAIRAVAN – OCTOBER 28th, 2020
EDITOR: KAT XIE
Background
According to the CDC, in 2019, approximately 34.1 million adults living in the United States smoked cigarettes regularly, making smoking a very prevalent public health crisis in our country today. Undeniably, smoking causes many significant health issues for a person, such as an increased risk of death, deteriorated lungs, and cardiovascular disease. As a result, the question we have to ask ourselves is what policy we can implement in order to reduce smoking among adults. One such answer to this question could be to raise federal taxes on cigarettes, which could potentially disincentivize people from buying more.
Whether or not cigarettes are an elastic or inelastic good is still somewhat unclear. Using data from Spain between 2002 to 2016, cigarettes are, in the long-run, an elastic good, and the authors suggest policymakers can increase taxes and central prices to influence the choice of buying cigarettes. On the other hand, an article written in 1999 by professor Sam Wylie at the Tuck School of Business, Dartmouth suggests that cigarettes are indeed inelastic goods and notes the deadweight loss is great. As a result, whether or not raising taxes on cigarettes will reduce smoking is still obscure.
Data
I decided to look at historical data from the year 1995 to see the effect of prices and taxes on cigarettes really did reduce the consumption of cigarettes. The dataset I used is from the Applied Econometrics with R package, and it contains data on real prices of cigarette packs, real excise taxes on cigarette packs, and the average amount of cigarette packs bought in a year—this dataset also encompasses all 50 states, and so it gives us a holistic picture of the United States as a whole.
Although the data is from 1995, generally speaking, the results could still have policy implications on how an increase in cigarette taxes could influence consumer behavior today.
Method
I created the following models:
- RealPrice = ꞵ₀ + ꞵ₁RealExciseTax + ε
- Packs = ꞵ₀ + ꞵ₁RealPrice + ꞵ₂RealExciseTax + ε
- Packs = ꞵ₀ + ꞵ₁RealPrice + ε
- Packs = ꞵ₀ + ꞵ₂RealExciseTax + ε
RealPrice is the price of a cigarette pack in 1995 dollars. RealExciseTax is the dollar amount of the sales tax placed on a pack of cigarettes, again adjusted for 1995 dollars. Packs is the variable I use to denote the number of cigarette packs bought per capita in 1995. ꞵ₀ is the y-intercept of the linear regression equations I use in my models. ꞵ₁ and ꞵ₂ are coefficients of a certain variable in my models. ε stands for the error in my model.
Discussion
The first model looks at the relationship between RealPrice and RealExciseTax. If we can deduce that an increase in taxes is correlated with prices, then it is very likely that, all else held constant, there is a causal relationship here.
In the second model, I look at the impact of both prices and taxes on the number of packs bought. This is the model I will use to determine if the effect of a change in prices on cigarette pack consumption drowns out the effect of a change in taxes on cigarette pack consumption, meaning the change in prices has a more significant effect.
In the third model, I solely look at the relationship between prices and packs. Because the second model also accounts for tax, I must isolate the effect of a change in price on a change in consumption in the third model. The fourth model simply isolates the impact of a rise in taxes on packs, similar to the third model. The third and fourth models allow me to look at the individual effects of the two variables RealPrice and RealExciseTax on Packs to determine if one has more influence than the other.
The final section of the discussion is about elasticity, in which I use the data from 1995 to calculate the elasticity coefficient to show the effect of price changes on quantity demanded.
Model 1
First, we must confirm that there is a strong relationship between RealPrice and RealExciseTax.
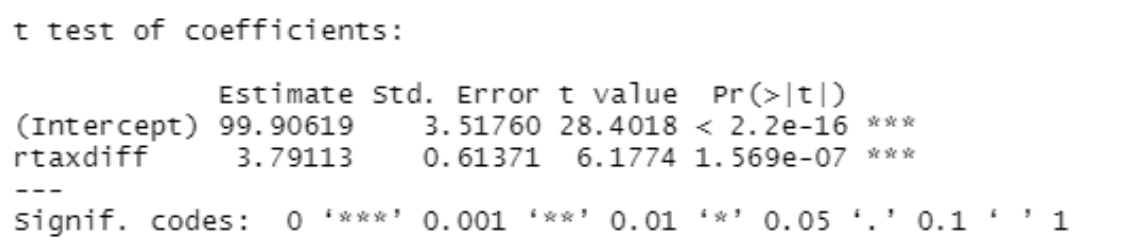
Given that the variable and y-intercept are statistically significant (p-values of 1.569e^-7 and 2.2e^-16, respectively), it is clear that as taxes rise, prices rise as well and that just accounting for tax increases in price increases is enough. The OLS shows us that for every $1 tax increase, there is an associated $3.79 increase in real prices for cigarette packs.
Model 2
The second model observes the relationship between Packs, RealPrice, and RealExciseTax.
A t-test of the second model is shown below:
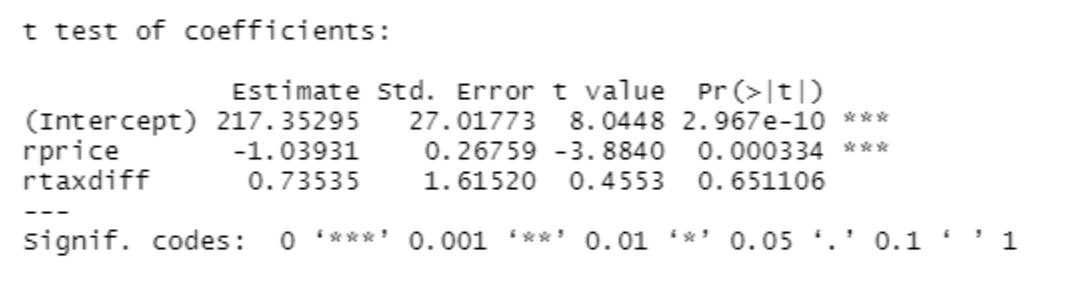
Our results are statistically significant except for the tax difference variable (RealPrice has a p-value of 0.0003, but RealExciseTax has a p-value of 0.65). This is possibly because the tax difference is already accounted for in our price, and so RealPrice does indeed drown out RealExciseTax. In order to isolate each variable’s effects, I run the test again, but this time separating the effect of taxes and prices on cigarette pack consumption.
Model 3
The third model looks the relationship between Packs and RealPrice.
A t-test of the third model is shown below:
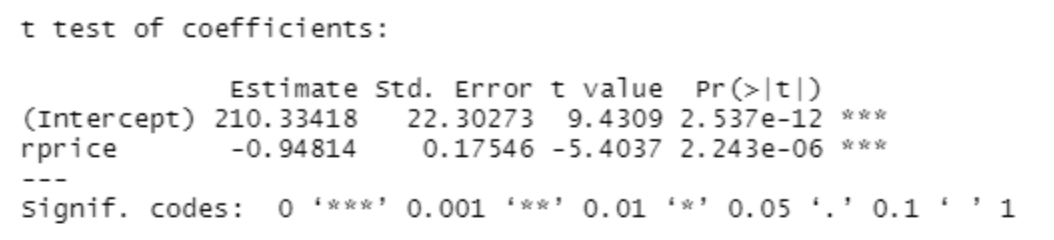
As we can see, our results are statistically significant (p-values are 2.243e^-6 for RealPrice and 2.537e^-12 for the y-intercept), and for every $1 increase in real prices, there seems to be, approximately, a one pack decrease in cigarette consumption. This relationship is also illustrated in the graph below:
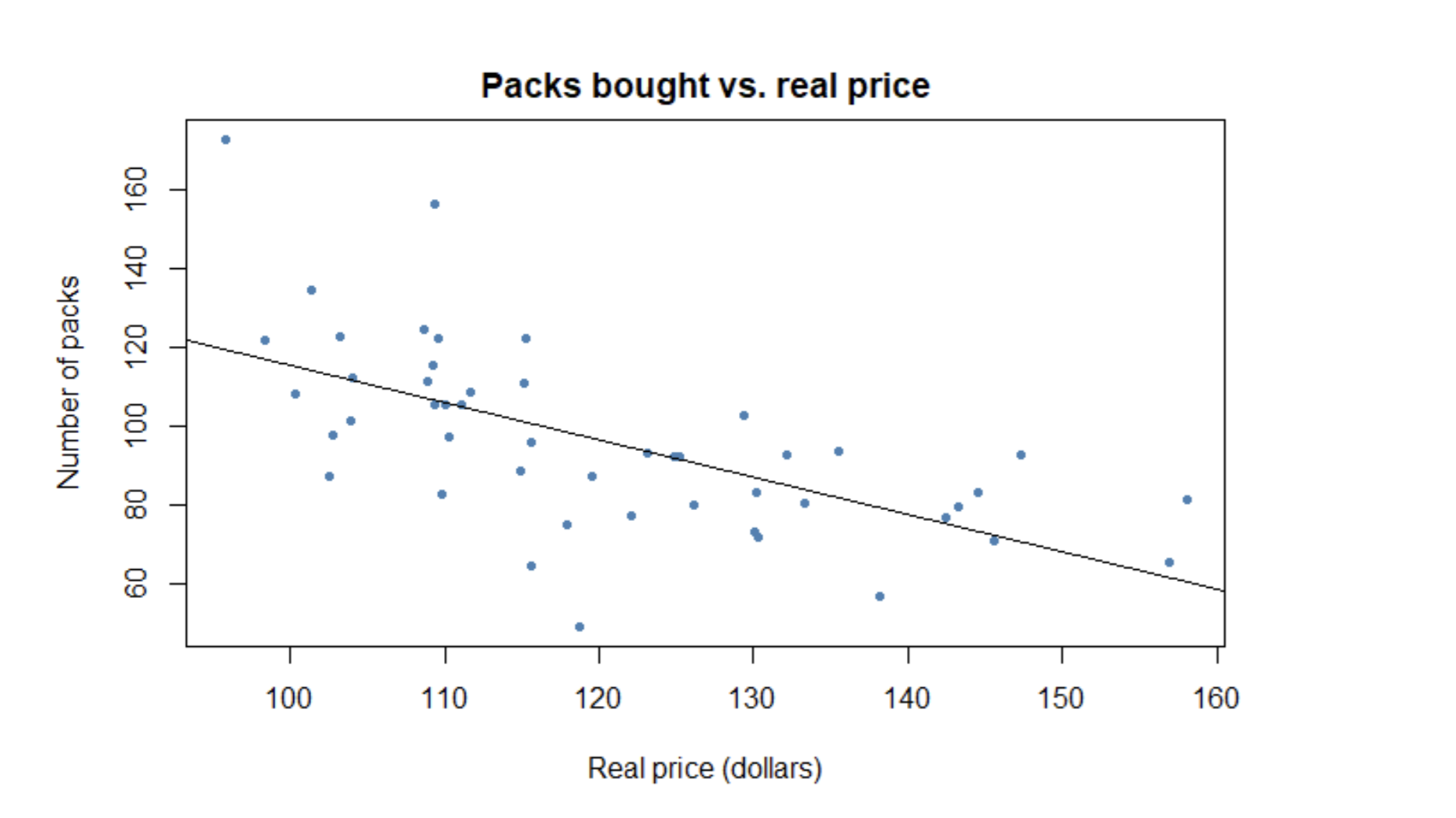
There is a somewhat strong negative correlation between real prices and packs bought, suggesting that an increase in prices could affect consumer behavior in the desired way.
Model 4
The fourth model looks at the relationship between Packs and RealExciseTax.
A t-test of the fourth model is shown below:
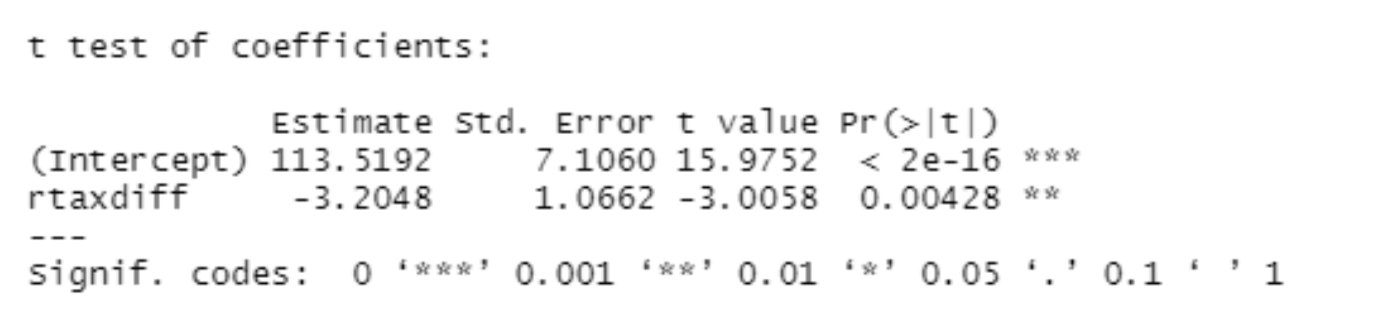
Our results are statistically significant to the point where p<0.001 (0.04 for RealExciseTax and 2e^-16 for the y-intercept), which is still very significant. This shows us that for every $1 increase in real taxes, there is an estimated three pack decrease in cigarette consumption.
Elasticity
Using the below formula for elasticity, we calculate that the price elasticity of demand for cigarettes is approximately 0.95, which shows that this good is very close to unit elastic. First, I took the mean of RealPrice and and Packs—let us call those variables RealPricemean and Packsmean. We compute (RealPricemean + 3) / (RealPricemean) for (%Δ𝐏) because each $1 increase in taxes corresponds to a $3 increase in prices, so we add 3. On the other hand, we calculate (Packsmean – 3) / (Packsmean) for (%Δ𝑸) because this is the corresponding decrease in packs demanded after the tax (and subsequent price) increase. We divide (%Δ𝑸) by (%Δ𝐏) to get our elasticity of 0.95.
Ɛ = | (%Δ𝑸) / (%Δ𝐏) |
Ɛ is the variable we use to show the elasticity coefficient. (%Δ𝑸) is the percent change in quantity demanded for a good. (%Δ𝐏) is the percent change in price for a good. We divide (%Δ𝑸) by the
(%Δ𝐏) in absolute value to find our elasticity coefficient.
Conclusion
Based on the data presented in 1995, our findings in the first model were that if there is a $1 increase in taxes, there is an approximate $3-4 increase in prices for ciga
rette packs. This is consistent with the third model, which suggests that a $1 increase in prices leads to a one pack decrease in consumption. Thus, for every $1 increase in taxes, we will see a decrease in consumption of about 3 packs, which is what the fourth model shows us. On the topic of elasticity, what the results show us is that because cigarettes were unit elastic.
Even though the data was collected in 1995, these insights are important for health policy today because of the general principle that human behavior stays relatively consistent. This research shows that increasing taxes on cigarettes slightly could potentially reduce the amount of cigarettes an adult purchases. However, this alone will not solve the smoking crisis, as made evident above in the elasticity calculations—an increase in taxes will only have a minimal effect of the reduction of cigarette consumption. This policy is just the first step. We must implement other policies such as educational programs to prevent people from smoking and offer counseling programs to those who need help quitting in order to achieve a healthier society.
Featured image source: https://unsplash.com/photos/mVCIG2QHLyI
Disclaimer: The views published in this journal are those of the individual authors or speakers and do not necessarily reflect the position or policy of Berkeley Economic Review staff, the Undergraduate Economics Association, the UC Berkeley Economics Department and faculty, or the University of California, Berkeley in general.



